Übungsblätter/Arbeitsblätter Mathematik - Realschule 9. Klasse
Grafische bzw. geometrische Darstellungsformen gewinnen zunehmend an Bedeutung und fördern bei den Schülern der 9. Klasse die Fähigkeit zu abstrahieren. Offene Aufgabenstellungen sowie Variationen von Aufgaben und Lösungswegen fördern die Vernetzung und Vertiefung der Lerninhalte.
9. Klasse Schwerpunkte
Alle auswählen
Binomische Formeln
Gleichungssysteme
Knobelaufgaben
Permutation
Quadratische Ergänzung
Quadratische Funktionen
Quadratische Gleichungen
Satz des Pythagoras
Wahrscheinlichkeitsrechnung
Übungen und Klassenarbeiten
Arbeitsblatt: Übung 1150 -
Knobelaufgaben
Sechs interessante Knobelaufgaben sind zu lösen: Zahlenreihe, Logikrätsel, Würfelgebäude, Quadernetz und Zahlenstrahl. Die Aufgaben sind eher leicht zu lösen.
|
 |
Arbeitsblatt: Übung 1148 -
Knobelaufgaben
Sechs Knobelaufgaben sind zu lösen: Teilung eines Kreises, Melonenrätsel (Prozentrechnung), Logikaufgabe, Hundetreffen (Gleichungssystem), Denksportaufgabe und Zahlenreihe. Die Aufgaben sind vom Typ "mittelschwer".
|
 |
Arbeitsblatt: Übung 1141 -
Wahrscheinlichkeitsrechnung
-Permutation
In den gemischten Aufgaben zur Wahrscheinlichkeitsrechnung wird der gesamte Bereich abgedeckt. Für die Bearbeitung der acht Aufgaben ist das Beherrschen von Formeln ebenso gefragt wie das Zeichnen von Baumdiagrammen.
|
 |
Arbeitsblatt: Übung 1147 -
Knobelaufgaben
Sechs interessante Denksportaufgaben: Verwandtschaftsverhältnis, Holzwurm im Würfel, Zahlenfolge, parallele Linien, Entfernungsaufgabe, Würfeloberfläche. Die Aufgaben sinf zum Teil schwer zu lösen.
|
 |
Arbeitsblatt: Übung 1132 -
Quadratische Funktionen
Übung zu den quadratischen Funktionen: Schnittpunkte von zwei Parabeln.
|
 |
Arbeitsblatt: Übung 1139 -
Wahrscheinlichkeitsrechnung
Inhalt der Übung sind Berechnungen mehrstufiger Zufallsexperimente: Mehrmaliges Drehen eines Glücksrades und Ziehen von farbigen Kugeln aus Urnen und Lostrommeln stehen im Mittelpunkt der Aufgaben.
|
 |
Arbeitsblatt: Übung 1129 -
Quadratische Funktionen
Übung zu den quadratischen Funktionen: Scheitelpunktform und Normalform einer Parabel.
|
 |
Arbeitsblatt: Übung 1138 -
Wahrscheinlichkeitsrechnung
Es geht um das Berechnen mehrstufiger Zufallsexperimente (Grundwissen). Aufgaben zu mehrfachem Münzwurf, mehrmaligem Drehen eines Glücksrades und Ziehen von mehreren Kugeln aus Urnen sind zu lösen. Auch Baumdiagramme sind verlangt.
|
 |
Arbeitsblatt: Übung 1140 -
Wahrscheinlichkeitsrechnung
-Permutation
Im Mittelpunkt steht die Permutation. Es sollten die benötigten Kombinatorik-Formeln (Fakultät, n über k) beherrscht werden, um die Vertauschungsmöglichkeiten in den zahlreichen Aufgaben berechnen zu können.
|
 |
Schulaufgabe Übung 1111 -
Quadratische Funktionen
Schwerpunkte dieser Schulaufgabe über die quadratischen Funktionen: Normalparabeln zeichnen, Koordinaten des Scheitelpunkts berechnen, Schnittpunkte von Parabeln (auch mit Geraden), Nullstelle berechnen, Normalform und Scheitelpunktsform, Funktionsgleichung und Diskriminante.
|
 |
Schulaufgabe Übung 1109 -
Gleichungssysteme
8 Aufgaben zu linearen Gleichungssystemen: Additions- und Subtraktionsverfahren, Einsetzverfahren, Gleichsetzungsverfahren, zeichnerische und rechnerische Lösung werden verlangt.
|
 |
Arbeitsblatt: Übung 1128 -
Quadratische Funktionen
Übung zu den quadratischen Funktionen: Schnittpunkte einer Parabel mit den Achsen.
|
 |
Arbeitsblatt: Übung 1151 -
Satz des Pythagoras
Vier zum Teil anspruchsvolle Übungsaufgaben zum rechtwinkligen Dreieck (Satz des Pythagoras). Dessen Anwendung soll anhand geeigneter Zerlegungen von Kreis, Rechteck und Trapez geübt werden.
|
 |
Arbeitsblatt: Übung 1127 -
Quadratische Funktionen
Übung zu den quadratischen Funktionen: Verschieben der Normalparabel.
|
 |
Arbeitsblatt: Übung 1185 -
Gleichungssysteme
Sechs Übungsaufgaben zu den linearen Gleichungssystemen. Schwerpunkte sind die drei Lösungsverfahren, die rechnerische und zeichnerische Lösung sowie die Anwendung von Gleichungssystemen in Textaufgaben.
|
 |
Arbeitsblatt: Übung 1130 -
Quadratische Funktionen
Übung zu den quadratischen Funktionen: Erstellen der Parabelgleichung aus gegebenen Punkten.
|
 |
Arbeitsblatt: Übung 1131 -
Quadratische Funktionen
Übung zu den quadratischen Funktionen: Schnittpunkte einer Parabel mit einer Geraden.
|
 |
Arbeitsblatt: Übung 1187 -
Gleichungssysteme
Acht Übungsaufgaben zu den linearen Gleichungssystemen. Schwerpunkte sind rechnerisches und zeichnerisches Lösungsverfahren und die Anwendung von Gleichungssystemen in Textaufgaben.
|
 |
Arbeitsblatt: Übung 1186 -
Gleichungssysteme
Sieben Übungsaufgaben zu den linearen Gleichungssystemen. Schwerpunkte sind das rechnerische Lösungsverfahren, die Lage von Geraden beim zeichnerischen Verfahren sowie die Anwendung von Gleichungssystemen in Textaufgaben.
|
 |
Arbeitsblatt: Übung 1107 -
Quadratische Funktionen
Schwerpunkte: Normalparabeln; Ermitteln der Funktionsgleichung; Zeichnen von Parabeln; Scheitelpunktsform und Normalform; Berechnung der Nullstellen; Berechnung der Schnittpunkte zweier Parabeln; Schnittpunkt von Parabel und Gerade; Wertetabelle;
|
 |
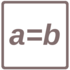Arbeitsblatt: Übung 1006 -
Binomische Formeln
Quadratische Gleichungen sollen unter Verwendung der binomischen Formeln umgeformt werden.
|
 |
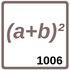Arbeitsblatt: Übung 1008 -
Quadratische Ergänzung
Bestimmen Sie die Lösung(en) der quadratischen Gleichungen mit Hilfe der quadratischen Ergänzung.
|
 |
Arbeitsblatt: Übung 1010 -
Quadratische Gleichungen
Bestimmen Sie die Lösungen der quadratischen Gleichungen mit Hilfe der allgemeinen Lösungsformel.
|
 |
Arbeitsblatt: Übung 1009 -
Quadratische Ergänzung
Bestimmen Sie die Lösung(en) der quadratischen Gleichungen mit Hilfe der quadratischen Ergänzung.
|
 |
Arbeitsblatt: Übung 1007 -
Quadratische Gleichungen
Bestimmen Sie die Lösungen der quadratischen Gleichungen mit Hilfe der allgemeinen Lösungsformel.
|
 |
Möchten Sie alle angezeigten Lösungen auf einmal in den Einkaufswagen legen? Sie können einzelne Lösungen dort dann wieder löschen.
*) Gesamtpreis für alle Dokumente (inkl. MwSt.): 30.00 €. Ggf. erhalten Sie Mengenrabatt auf Ihren Einkauf.
*) Gesamtpreis für alle Dokumente (inkl. MwSt.): 30.00 €. Ggf. erhalten Sie Mengenrabatt auf Ihren Einkauf.
Vielleicht interessieren Sie sich auch für die Aufgaben in anderen Fächern:
Physik - Realschule 9. Klasse Übungsaufgaben
Physik - Realschule 9. Klasse Übungsaufgaben
Auszug aus dem Lehrplan [Mathematik Realschule klasse_9] (BY):
Systeme linearer Gleichungen mit zwei Variablen lösen [Gleichungssysteme]
quadratische Gleichungen: Lösungsformel, Bedeutung der Diskriminante
Koordinaten der Schnittpunkte von Funktionsgraphen, Tangentialprobleme
in der Menge IR der reellen Zahlen rechnen
Definition der Quadratwurzel kennen und anwenden
einfache Termumformungen mit Quadratwurzeln
[Quadratische Funktionen]
Graphen und Eigenschaften von quadratischen Funktionen, Scheitelform
Gleichungen von Parabeln ermitteln, Parameterverfahren
Flächeninhalte ebener Figuren insbesondere auch mithilfe zweireihiger Determinanten
Umfang und Flächeninhalt von Kreisen, Mantel- bzw. Oberfläche und Volumen von Prismen, Pyramiden, geraden Kreiszylindern und Kreiskegeln sowie von Kugeln
Abbildung durch zentrische Streckung anwenden
Streckenlängen mit dem Vierstreckensatz bestimmen
Berechnungen mithilfe von Vektoren
Ähnlichkeit von Dreiecken
mithilfe der Flächensätze am rechtwinkligen Dreieck Streckenlängen berechnen
Pfadregeln und ihre Anwendung
Quelle: http://www.isb.bayern.de
[Stand: 05/2012]
Hinweis: Die Lerninhalte sind ein Auszug aus dem Lehrplan für bayerische Schulen. In anderen deutschen Bundesländern existieren teilweise weitere Schularten. Diese sind z.B.:
Systeme linearer Gleichungen mit zwei Variablen lösen [Gleichungssysteme]
quadratische Gleichungen: Lösungsformel, Bedeutung der Diskriminante
Koordinaten der Schnittpunkte von Funktionsgraphen, Tangentialprobleme
in der Menge IR der reellen Zahlen rechnen
Definition der Quadratwurzel kennen und anwenden
einfache Termumformungen mit Quadratwurzeln
[Quadratische Funktionen]
Graphen und Eigenschaften von quadratischen Funktionen, Scheitelform
Gleichungen von Parabeln ermitteln, Parameterverfahren
Flächeninhalte ebener Figuren insbesondere auch mithilfe zweireihiger Determinanten
Umfang und Flächeninhalt von Kreisen, Mantel- bzw. Oberfläche und Volumen von Prismen, Pyramiden, geraden Kreiszylindern und Kreiskegeln sowie von Kugeln
Abbildung durch zentrische Streckung anwenden
Streckenlängen mit dem Vierstreckensatz bestimmen
Berechnungen mithilfe von Vektoren
Ähnlichkeit von Dreiecken
mithilfe der Flächensätze am rechtwinkligen Dreieck Streckenlängen berechnen
Pfadregeln und ihre Anwendung
Quelle: http://www.isb.bayern.de
[Stand: 05/2012]
Hinweis: Die Lerninhalte sind ein Auszug aus dem Lehrplan für bayerische Schulen. In anderen deutschen Bundesländern existieren teilweise weitere Schularten. Diese sind z.B.:
- Regionalschule (Rheinland-Pfalz, Mecklenburg-Vorpommern)
- Erweiterte Realschule (Saarland)
- Realschule plus (Rheinland-Pfalz)
- Mittelschule (Sachsen, Bayern)
- Oberschule (Baden-Württemberg, Brandenburg, Bremen, Niedersachsen)
- Regelschule (Thüringen)
- Sekundarschule (Sachsen-Anhalt, NRW)
- Gemeinschaftsschule (Berlin)
- Gesamtschule (diverse Bundesländer)