Einheit 02: Schnittpunkte einer Parabel mit den Koordinaten-Achsen

Online-Lehrgang für Schüler

Einleitung
Lösen von Aufgaben "Schnittpunkt mit der y-Achse"
Lösen von Aufgaben "Schnittpunkt mit der x-Achse"
Die Diskriminante
Beispiel-Aufgabe
Download Übungseinheit 02

Weitere Übungseinheiten zu: Quadratische Funktionen

Einleitung

Bei den folgenden Aufgaben sollen Punkte berechnet werden, in denen eine Parabel die Koordinatenachsen schneidet. Bei jeder Aufgabe sollen jeweils beide Achsenabschnitte, also sowohl der Schnittpunkt mit der y-Achse als auch der Schnittpunkt mit der x-Achse (Nullstellen) bestimmt/berechnet werden.

Zu den Aufgaben gibt es auch ausführliche Lösungen, zum Teil mit dem gezeichneten Graphen als Kontrolle, und mit den entsprechenden Lösungswegen.

Lösen von Aufgaben "Schnittpunkt mit der y-Achse"

Ist die allgemeine Form einer quadratischen Funktion (y=ax²+bx+c) gegeben, so ist der Schnittpunkt der Parabel mit der y-Achse (=y-Achsenabschnitt) das Absolutglied c. Der y-Wert der Koordinaten des Schnittpunktes kann dann einfach abgelesen werden.
Der x-Wert der Koordinaten des Schnittpunktes ist immer 0.
Ist die quadratische Funktion in der Scheitelform gegeben, so wird sie in die Normalform umgewandelt oder es wird sofort x = 0 eingesetzt.

Lösen von Aufgaben "Schnittpunkt mit der x-Achse"

Die y-Koordinate eines Schnittpunktes mit der x-Achse ist Null. Y wird also gleich Null gesetzt.
Die Lösung erfolgt dann über die p/q-Formel oder die „Mitternachtsformel“ (=allgemeine Lösungsformel).
Bei diesen Schnittpunkten spricht man auch von Nullstellen.

Die Diskriminante

Die Diskriminante ist ein Rechenausdruck, der Aussagen über Zahl und Art der Lösungen einer algebraischen Gleichung ermöglicht. Sie ist der Ausdruck unter der Wurzel in der p/q Formel,
also :

D = (p/2)² - q

oder in der „Mitternachtsformel“, also:

D = b² - 4ac

Mit Hilfe der Diskriminante kann eine Aussage darüber getroffen werden, wie viele Lösungen eine quadratische Gleichung hat. Es gilt:
D > 0 → es gibt zwei verschiedene reelle Lösungen
D = 0 → es gibt eine reelle Lösung
D < 0 → es gibt keine reelle Lösung

Arbeiten mit dieser Übungseinheit

Es empfiehlt sich, die hier vorliegenden Aufgaben systematisch durchzuarbeiten und mit den angebotenen Lösungen zu vergleichen. Alle Übungen enthalten sehr viele Aufgabenstellungen, in denen mögliche Fragestellungen angesprochen sind, wie sie immer wieder in Prüfungsarbeiten und Schulaufgaben auftauchen.

Beispiel-Aufgabe: Achsenschnittpunkte berechnen

Auszug aus der Aufgabenstellung zur Übungseinheit 02:

parabel-schnittpunkt-x-achse

Auszug aus der Lösung:
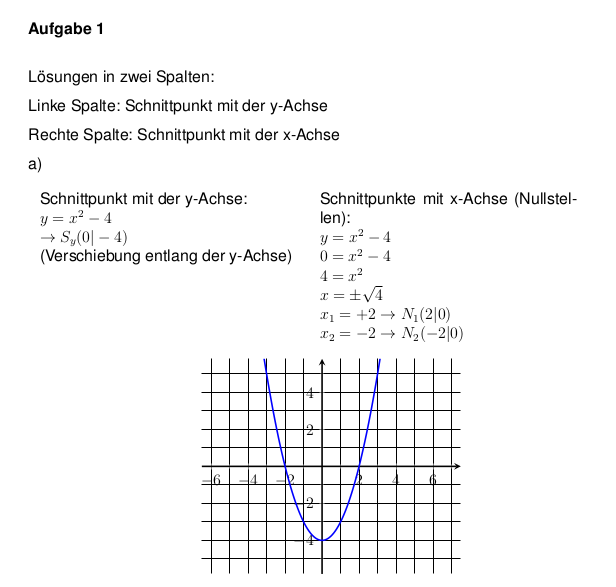
parabel-schnittpunkt-x-achse

Download der Übungseinheit

Die Übungseinheit und die zugehörigen Lösungen stehen zum Download bereit. Wie Sie die PDF-Dokumente selbst zur eigenen Vorbereitung bzw. in Ihrem Unterricht nutzen dürfen, lesen Sie bitte bei Lizenzen.

Download der Aufgabenblätter

3 Seiten mit Übungsaufgaben zu den Themen: