aufgaben.schulkreis.de
Mathematik     Deutsch     Physik     HSU     Wissen
(0)  Einkaufswagen

Home
  |  
Aufgaben
  |  
Aufg.sammlungen
  |  
Papier
  |  
Lesetests
  |  
Ferien
  |  
Wetter
  |  
Üben
  |  
Unterr.material
  |  
Klassenarbeiten

Schwerpunkte 8. Klasse Addieren Binomische Formeln Bruchrechnung Dividieren Funktionsgraphen Gleichungssysteme Knobelaufgaben Kopfrechnen Lineare Funktionen Multiplizieren Permutation Quadratische Ergänzung Quadratische Funktionen Quadratische Gleichungen Subtrahieren Terme Wahrscheinlichkeitsrechnung
Spezielle Übungen Knobelaufgaben Lineare Funktionen Prozentrechnung Start: Online-Lehrgang: Quadratische Funktionen Teil1: Verschieben der Normalparabel, Nullstellen Teil2: Schnittpunkte der Parabel mit x- und y-Achse Teil3: Parabel: Scheitelpunktform und Normalform Teil4: Parabelgleichung ermitteln aus zwei Punkten Teil5: Schnittpunkte Parabel-Gerade bestimmen Teil6: Schnittpunkte zweier Parabeln berechnen Wahrscheinlichkeitsrechnung
Ihr Einkauf   Einkaufswagen (0 Artikel)

Lineare Funktionen - Übungen, Arbeitsblätter

Lineare Funktionen: Übungen zum Ausdrucken, mit Lösung

Ein wichtiger Bestandteil der Mathematik sind Funktionen. Eine Art davon ist die lineare Funktion. Sie ist eine sehr wichtige und grundlegende Funktionsart. Die vorliegende Übungsreihe beschäftigt sich mit dieser Thematik.

Grundlegende Bedeutung linearer Funktionen
Voraussetzung für das erfolgreiche Arbeiten mit linearen Funktionen
Intention der Übungsreihe
Aufbau und Verwendung der Übungsblätter
Weitere Übungsaufgaben Mathe

Grundlegende Bedeutung linearer Funktionen

Die Beschäftigung mit linearen Funktionen ist in den Mathematik-Lehrplänen der weiterführenden Schulen (Mittelschule 9./10. Jahrgangsstufe, Realschule 8/9. bzw. Gymnasium 8. Jahrgangsstufe) vorgeschrieben.
Auch ist der Umgang mit und das gedankliche Durchdringen von Funktionen, in unserem Fall von Funktionen ersten Grades, von grundlegender Bedeutung für den Schüler, da ihm in der realen Welt immer wieder Beziehungen zwischen zwei Mengen begegnen.
Mathematisch ausgedrückt bedeutet das: Eine Funktion ist eine Zuordnung, bei der jedem Element x der Definitionsmenge (Definitionsbereich) genau ein Element y der Wertemenge (Wertebereich) zugeordnet ist. Mit anderen Worten: Bei einer Funktion ist jedem x-Wert genau ein y-Wert zugeordnet.

Da lineare Funktionen auch immer wieder in Prüfungen, Schulaufgaben oder Proben abgefragt werden, ist eine Auseinandersetzung mit diesem Lerninhalt unerlässlich.

Voraussetzung für das erfolgreiche Arbeiten mit linearen Funktionen

Bei der Berechnung linearer Funktionen wird erwartet, dass die Schüler das Lösen linearer Gleichungen durch gezielte Äquivalenzumformungen beherrschen. Auch der sichere Umgang mit negativen Zahlen und die Beherrschung des Bruchrechnens sind unerlässliche Voraussetzung, um rechnerisch die in diesem Bereich gestellten Fragen und Arbeitsaufträge beantworten und lösen zu können.
Die Übungsreihe bietet den Schülern die Möglichkeit, diese Grundvoraussetzungen immer wieder zu üben und zu verinnerlichen, indem im Lösungsteil der jeweilige Lösungsweg klar strukturiert ist.
Lineare Funktionen:

Eine lineare Funktionsgleichung hat die Form

y = mx + t oder f (x) = mx + t

y = die abhängige Variable: Es ist der Funktionswert, der davon abhängt, welchen Wert man für x einsetzt.

m = Steigung
m > 0: Die Gerade steigt, die Steigung ist positiv.
m < 0: Die Gerade fällt, die Steigung ist negativ.
m = 0: Die Gerade ist waagrecht (Sonderfall: konstante Funktion), parallel zur x-Achse

x = die unabhängige Variable, das Funktionsargument

t = y-Achsenabschnitt
t > 0: Die Gerade ist nach oben verschoben.
t < 0: Die Gerade ist nach unten verschoben.
t = 0: Die Gerade verläuft durch den Koordinatenursprung (= Nullpunkt).

Der Graph einer linearen Funktion ist eine Gerade. Sie kann in ein Koordinatensystem gezeichnet werden.
Dies sind die Grundlagen zum Thema "Lineare Funktionen". Sie haben in der vorliegenden Übungsreihe ihren festen Platz.

Intention der Übungsreihe

Mit der vorliegenden Übungsreihe können Schüler ihr Wissen und ihre Fähigkeiten im Umgang mit linearen Funktionen anwenden und vertiefen.
Die Aufgabenblätter erstrecken sich über die wichtigsten Aspekte der linearen Funktionen. Die einzelnen Teile der Übungsreihe sind so aufgebaut, dass fortschreitend alle Themenbereiche linearer Funktionen behandelt werden. So wird den Schülern die Möglichkeit geboten, ergänzend zum jeweils im Unterricht behandelten Thema, gezielte Übungsaufgaben zu bearbeiten.
Erwähnt werden soll auch, dass zu Beginn einer Übungseinheit ein gewisses Grundwissen abgefragt wird. Damit soll dem Schüler der jeweilige Lernstoff noch einmal verdeutlicht werden.
Zu allen Teilen der Übungsreihe werden ausführliche, klar strukturierte und von Lehrern ausgearbeitete, schülergerechte Lösungen angeboten.
Durch den gezielten Aufbau der Übungsreihe mit ihren einzelnen Einheiten ist es auch denkbar, dass die angebotenen PDFs im Home-schooling bzw. im Distance-learning eingesetzt werden können.

Verwendung der Übungsblätter

Mit unseren Übungsaufgaben können lineare Funktionen ideal trainiert werden. Die Aufgabenblätter erstrecken sich über diverse Aspekte der Rechnung mit linearen Funktionen und bauen aufeinander auf.


Verwendung:
Alle Aufgabenblätter dürfen Sie ausdrucken und zu Hause oder im Unterricht gemäß unseren Nutzungsbedingungen einsetzen.

Lineare Funktionen Übungsreihe, Teil 1


Begriffe, Darstellung, Wertetabellen

Dies ist Teil 1 der Übungsreihe "Lineare Funktionen". Inhalte: * Wichtige Begriffe zu linearen Funktionen * Wertetabellen

Vorschau   |   Download PDF   |   Download Lösung 		 

Lineare Funktionen Übungsreihe, Teil 2


Bestimmung der Funktionsgleichung, Zeichnen von Geraden

Dies ist Teil 2 der Übungsreihe "Lineare Funktionen". Inhalte: * Bestimmen von Funktionsgleichungen durch Ablesen von Graphen * Zeichnen von Geraden in Koordinatensysteme * Steigungsdreieck * Ursprungsgeraden * Parallele Geraden

Vorschau   |   Download PDF   |   Download Lösung 		 

Lineare Funktionen Übungsreihe, Teil 3


Funktionsgleichung, Abstand zweier Punkte

Dies ist Teil 3 der Übungsreihe "Lineare Funktionen". Inhalte: * Bestimmen von Funktionsgleichungen linearer Funktionen bei gegebenem Steigungsfaktor und y-Abschnitt * Abstand zweier Punkte * Parallele Geraden * Umformen von Funktionsgleichungen in die Normalform

Vorschau   |   Download PDF   |   Download Lösung 		 

Lineare Funktionen Übungsreihe, Teil 4


Funktionsgleichung aus Steigung und Punkt, senkrechte Geraden

Dies ist Teil 4 der Übungsreihe "Lineare Funktionen". Inhalte: * Ermitteln der Funktionsgleichung linearer Funktionen bei gegebenem Steigungsfaktor und einem Punkt auf der Geraden * Ermitteln der Funktionsgleichung bei gegebenem y-Achsenabschnitt und einem Punkt auf der Geraden * Berechnen und Zeichnen der Senkrechten zu Geraden

Vorschau   |   Download PDF   |   Download Lösung 		 

Lineare Funktionen Übungsreihe, Teil 5


Funktionsgleichung aus zwei Punkten, Koordinaten berechnen

Dies ist Teil 5 der Übungsreihe "Lineare Funktionen". Inhalte: * Ermitteln der Funktionsgleichung aus zwei gegebenen Punkten * Überprüfung der Lage von Punkten * Koordinaten von Punkten berechnen * Senkrechte und parallele Geraden

Vorschau   |   Download PDF   |   Download Lösung 		 

Lineare Funktionen Übungsreihe, Teil 6


Schnittpunkt zweier Geraden

Dies ist Teil 6 der Übungsreihe "Lineare Funktionen". Inhalte: * Berechnen des Schnittpunktes zweier Geraden * Berechnen der Nullstelle

Vorschau   |   Download PDF   |   Download Lösung 		 

Lineare Funktionen Übungsreihe, Teil 7


Spiegelung an x- und y-Achse

Dies ist Teil 7 der Übungsreihe "Lineare Funktionen". Inhalte: * Spiegelung an x- und y-Achse * Bestimmen von Funktionsgleichungen * Berechnen von Senkrechten und Nullstellen

Vorschau   |   Download PDF   |   Download Lösung 		 

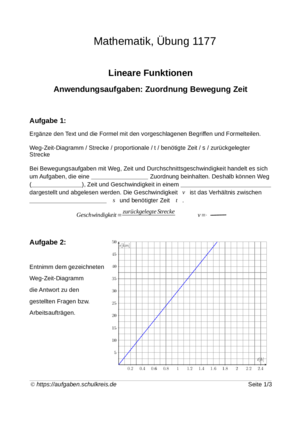
Lineare Funktionen Übungsreihe, Teil 8


Bewegungsaufgaben, Zuordnung Bewegung/Zeit

Dies ist Teil 8 der Übungsreihe "Lineare Funktionen". Inhalte: * Anwendungsaufgaben * Weg-Zeit-Diagramm * Weg, Strecke, Geschwindigkeit

Vorschau   |   Download PDF   |   Download Lösung 		 

Lineare Funktionen Übungsreihe, Teil 9


Zusammenfassende Übungsaufgaben

Dies ist Teil 9 der Übungsreihe "Lineare Funktionen". Inhalte: * Zusammenfassende Aufgaben, der gesamte Bereich der linearen Funktionen sollte zum Lösen beherrscht werden.

Vorschau   |   Download PDF   |   Download Lösung 		 



Möchten Sie alle angezeigten Lösungen auf einmal in den Einkaufswagen legen? Sie können einzelne Lösungen dort dann wieder löschen.

 

*) Gesamtpreis für alle Dokumente (inkl. MwSt.): 10.80 €. Ggf. erhalten Sie Mengenrabatt auf Ihren Einkauf.