Hier finden Sie Übungsaufgaben für Mathematik in der Realschule (5. 6. 7. 8. 9. 10. Klasse) zum Ausdrucken. Zahlreiche Aufgabenblätter stehen kostenlos als PDF Dateien zum Download bereit.

Die Schüler lernen, die geometrischen Grundfiguren zu erfassen, zu zeichnen und sie als Punktmengen zu verstehen. Anhand von Aufgaben aus dem Alltag festigen und vertiefen sie die Fertigkeit, mit Größen, Maßzahlen und Maßeinheiten zu rechnen und grundlegende mathematische Verfahren (z. B. den Dreisatz) bei der Lösung einfacher Probleme anzuwenden.

5. Klasse Schwerpunkte

Alle auswählen

Addieren

Kombinatorik allgemein

Tipp: Unsere 10-teilige Übungsreihe "Schritt für Schritt zum Übertritt" eignet sich gut zur Wiederholung des Vorjahresstoffs aus Klasse 4. Für weitere Inhalte zur Klasse 5 besuchen Sie deshalb bitte auch:
Übungsreihe Mathematik, Wiederholung für Klasse 5.

Übungen und Klassenarbeiten

Arbeitsblatt: Übung 1154 -

Kombinatorik allgemein

Knobelaufgaben

Realschule 5. Klasse - Übungsaufgaben Mathe allgemein

Die zum Teil anspruchsvollen Knobeleien erfordern neben dem sicheren Umgang mit den Mitteln der Grundschule (4.Klasse) auch die Fähigkeit, Sachverhalte mathematisch zu erfassen und zu beschreiben. Es sind sieben Aufgaben zu lösen, Schwerpunkt ist die Kombinatorik.

Vorschau 1154 | Download Aufgabe 1154 (PDF)

Download Lösung 1154

Arbeitsblatt: Übung 1064 -

Multiplizieren

Dividieren

Terme

Natürliche Zahlen

Klammerrechnung

Realschule 5. Klasse - Übungsaufgaben Arithmetik/Algebra

Das Aufstellen und Berechnen von Termen sind der Schwerpunkt dieser Arbeit. Neben Summen und Differenzen enthalten die Terme auch Produkte und Quotienten. Zwei Sachaufgaben bilden den Abschluss.

Vorschau 1064 | Download Aufgabe 1064 (PDF)

Download Lösung 1064

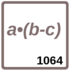Schulaufgabe Übung 1070 -

Multiplizieren

Dividieren

Ganze Zahlen

Realschule 5. Klasse - Schulaufgabe Arithmetik/Algebra

In Standard-Rechenaufgaben wird zunächst die Multiplikation und Division großer Zahlen abgefragt. Es folgen schwierigere Aufgaben, die die Fähigkeit zum vorteilhaften Rechnen voraussetzen. In fünf Textaufgaben sollen die Schüler dann als Text formulierte Aufgaben in Terme übersetzen und diese lösen. Den Abschluss bildet eine zum Thema passende Sachaufgabe.

Vorschau 1070 | Download Aufgabe 1070 (PDF)

Download Lösung 1070

Schulaufgabe Übung 1074 -

Natürliche Zahlen

Klammerrechnung

Realschule 5. Klasse - Schulaufgabe Mathe allgemein

Schwerpunkt dieser Arbeit sind die Multiplikation und Division natürlicher Zahlen. Auf eher einfache Berechnungsaufgaben folgen Platzhalteraufgaben und Termberechnungen. Textaufgaben, in denen Terme erst aufgestellt werden müssen, erfordern den sicheren Umgang mit den relevanten Fachbegriffen. Zum Abschluss soll der sichere Umgang mit dem Multiplizieren und Dividieren natürlicher Zahlen in zwei Sachaufgaben zur Anwendung kommen.

Vorschau 1074 | Download Aufgabe 1074 (PDF)

Download Lösung 1074

Schulaufgabe Übung 1072 -

Natürliche Zahlen

Realschule 5. Klasse - Schulaufgabe Mathe allgemein

Zum Lösen der Aufgaben ist ein vertieftes Verständnis der dezimalen Stellenschreibweise bis zur Billion erforderlich. Große Zahlen sollen in Dreiergruppen (E-, T-, Mio- Gruppe usw.) zerlegt werden. Große Zahlen müssen ausgeschrieben und Zahlbeziehungen - auch unter Zuhilfenahme der Stellenwerttafel - erkannt werden.

Vorschau 1072 | Download Aufgabe 1072 (PDF)

Download Lösung 1072

Schulaufgabe Übung 1071 -

Addieren

Subtrahieren

Natürliche Zahlen

Klammerrechnung

Realschule 5. Klasse - Lernzielkontrolle Mathe allgemein

Ziel dieser Lernzielkontrolle ist es, die Fähigkeit zum Rechnen auf der Grundlage eines gefestigten Zahlenverständnisses im Bereich der natürlichen Zahlen zu überprüfen. Es müssen Terme aufgestellt und berechnet werden, wobei insbesondere die Regeln der Addition und Subtraktion anzuwenden sind.

Vorschau 1071 | Download Aufgabe 1071 (PDF)

Download Lösung 1071

Arbeitsblatt: Übung 1063 -

Terme

Natürliche Zahlen

Klammerrechnung

Realschule 5. Klasse - Übungsaufgaben Arithmetik/Algebra

Natürliche Zahlen sollen schriftlich addiert und subtrahiert werden. Die Schüler sollen Terme durch geschicktes Umformen vorteilhaft berechnen können. In mehreren Textaufgaben müssen die Terme selbst aufgestellt werden.

Vorschau 1063 | Download Aufgabe 1063 (PDF)

Download Lösung 1063

Schulaufgabe Übung 1045 -

Größen

Realschule 5. Klasse - Lernzielkontrolle Mathe allgemein

Relativ anspruchsvolle Aufgaben zum Umrechnen zwischen benachbarten Einheiten sind Thema dieser Lernzielkontrolle. Die Größen "Geld", "Länge", "Masse" und "Zeit" sollten auch bei schwierigen Zahlenverhältnissen beherrscht werden. Dies ist Voraussetzung für das sichere Rechnen mit gängigen Größen und Maßeinheiten. Zwei Sachaufgaben bilden nach den Umrechnungsübungen den Abschluss. Dabei gilt es, die Fähigkeit im Umgang mit Größen, die in der Realität vorkommen, nachzuweisen.

Vorschau 1045 | Download Aufgabe 1045 (PDF)

Download Lösung 1045

Schulaufgabe Übung 1069 -

Multiplizieren

Dividieren

Natürliche Zahlen

Realschule 5. Klasse - Schulaufgabe Arithmetik/Algebra

Abgefragt wird in dieser Schulaufgabe in einfachen Aufgaben zunächst die Fähigkeit zum Umgang mit natürlichen Zahlen. Multiplikation und Division stehen im Mittelpunkt. Beim Ergänzen fehlender Zahlen/Ziffern müssen die Schüler dann ihr Gespür für die natürlichen Zahlen unter Beweis stellen. Des Weiteren ist vorteilhaftes Rechnen gefragt, um die weiteren Aufgaben in der gegebenen Zeit zu lösen. Abschließend folgen Textaufgaben und Sachaufgaben, um dem Gelernten einen Bezug zur Realität zu geben.

Vorschau 1069 | Download Aufgabe 1069 (PDF)

Download Lösung 1069

Schulaufgabe Übung 1067 -

Winkel

Realschule 5. Klasse - Schulaufgabe Geometrie

Anhand der Windrose (Kompassrose) wird die Kenntnis der Himmelsrichtungen abgefragt. Die Größe von Winkeln soll gemessen und Winkel sollen gezeichnet werden können. Dabei müssen die Fachbegriffe "spitzer Winkel", "stumpfer Winkel", "rechter Winkel", "überstumpfer Winkel" und "gestreckter Winkel" bekannt sein. Den Abschluss bildet eine Konstruktionsaufgabe im Koordinatensystem.

Vorschau 1067 | Download Aufgabe 1067 (PDF)

Download Lösung 1067

Schulaufgabe Übung 1019 -

Konstruktionen

Realschule 5. Klasse - Test Geometrie

Übungen zu geometrischen Konstruktionen: Quadrat, Sechseck mit Bestimmungsdreieck, Gerade, Kreis, gleichseitiges Dreieck und Rechteck sollten konstruiert werden können. 5 Aufgaben mit Teilaufgaben.

Vorschau 1019 | Download Aufgabe 1019 (PDF)

Download Lösung 1019

Schulaufgabe Übung 1075 -

Natürliche Zahlen

Realschule 5. Klasse - Schulaufgabe Mathe allgemein

Im Test soll das Verständnis der schriftlichen Normalverfahren (hier: Addieren und Subtrahieren) abgefragt werden. Auch ist der sichere Gebrauch der Fachbegriffe und Rechenoperationen zum Lösen der Aufgaben erforderlich. Den Abschluss bildet eine Sachaufgabe aus dem täglichen Leben.

Vorschau 1075 | Download Aufgabe 1075 (PDF)

Download Lösung 1075

Schulaufgabe Übung 1065 -

Winkel

Realschule 5. Klasse - Schulaufgabe Geometrie

Anhand der Windrose (Kompassrose) wird die Kenntnis der Himmelsrichtungen abgefragt. Die Größe von Winkeln soll gemessen und Winkel gezeichnet werden können. Dabei müssen die Fachbegriffe "spitzer Winkel", "stumpfer Winkel", "rechter Winkel", "überstumpfer Winkel" und "gestreckter Winkel" bekannt sein. Den Abschluss bildet eine Konstruktionsaufgabe im Koordinatensystem.

Vorschau 1065 | Download Aufgabe 1065 (PDF)

Download Lösung 1065

Schulaufgabe Übung 1046 -

Größen

Realschule 5. Klasse - Lernzielkontrolle - Schulaufgabe Mathe allgemein

Thema dieses Tests sind die Größen sowie die Umrechnungen zwischen benachbarten Einheiten. Diese Fertigkeit ist Voraussetzung dafür, dass in der Sachbezogenen Mathematik Aufgaben aus den Größenbereichen Geldwerte, Gewichte, Zeitspannen, Längen und Rauminhalte richtig gelöst werden. Neben mehreren Umrechnungsaufgaben dienen abschließend zwei Sachaufgaben dazu, den Umgang mit Größen, die in der Realität vorkommen, zu überprüfen.

Vorschau 1046 | Download Aufgabe 1046 (PDF)

Download Lösung 1046

Schulaufgabe Übung 1057 -

Addieren

Subtrahieren

Natürliche Zahlen

Realschule 5. Klasse - Schulaufgabe Mathe allgemein

Der Test behandelt die Addition und Subtraktion von natürlichen Zahlen. Zwei Zahlenmauern sowie zwei Zauberquadrate sollen zunächst gelöst werden. Des Weiteren sollten Assoziativgesetz und Kommutativgesetz bekannt sein, um Terme gliedern und berechnen zu können. Am Ende des Tests stehen drei Textaufgaben und eine Sachaufgabe an.

Vorschau 1057 | Download Aufgabe 1057 (PDF)

Download Lösung 1057

Schulaufgabe Übung 1066 -

Winkel

Realschule 5. Klasse - Schulaufgabe Geometrie

Vorschau 1066 | Download Aufgabe 1066 (PDF)

Download Lösung 1066

Schulaufgabe Übung 1018 -

Konstruktionen

Realschule 5. Klasse - Test Geometrie

Konstruktionen mit Winkel und Lineal sind gefordert: Parallele, Kreis, Lot, Winkelhalbierende, Mittelsenkrechte, Parallelogramm sollen in x-y-Koordinatensystemen konstruiert werden.

Vorschau 1018 | Download Aufgabe 1018 (PDF)

Download Lösung 1018

Schulaufgabe Übung 1056 -

Natürliche Zahlen

Realschule 5. Klasse - Schulaufgabe Mathe allgemein

Im Mittelpunkt dieser Probe stehen die natürlichen Zahlen. Neben dem Ablesen von Werten aus dem Zahlenstrahl und einem Balkendiagramm soll die Darstellung von Zahlen mit Hilfe von Zehnerpotenzen (Potenzschreibweise) beherrscht werden. Der Begriff der Primzahl soll bekannt sein, den Abschluss bilden drei Zahlenfolgen-Aufgaben.

Vorschau 1056 | Download Aufgabe 1056 (PDF)

Download Lösung 1056

Arbeitsblatt: Übung 1062 -

Terme

Natürliche Zahlen

Realschule 5. Klasse - Übungsaufgaben Arithmetik/Algebra

Thema der Übungsarbeit ist der Umgang mit natürlichen Zahlen. Neben der Darstellung mittels Zehnerpotenzen sollen Zahlen auch gerundet (aufgerundet und abgerundet) werden. Es folgt zuletzt eine Zahlenfolgenaufgabe.

Vorschau 1062 | Download Aufgabe 1062 (PDF)

Download Lösung 1062

Möchten Sie alle angezeigten Lösungen auf einmal in den Einkaufswagen legen? Sie können einzelne Lösungen dort dann wieder löschen.

^*) Gesamtpreis für alle Dokumente (inkl. MwSt.): 22.80 €. Ggf. erhalten Sie Mengenrabatt auf Ihren Einkauf.

Vielleicht interessieren Sie sich auch für die Aufgaben in anderen Fächern:
Deutsch - Realschule 5. Klasse Übungsaufgaben

Auszug aus dem Lehrplan [Mathematik Realschule klasse_5] (BY):

Anordnung der natürlichen Zahlen; Zahlenhalbgerade; die Beziehungen < und >
Das Dezimalsystem als ein Stellenwertsystem; Potenzschreibweise von Stufenzahlen; Runden

Addition und Subtraktion; schriftliche Verfahren; Summen und Differenzen
Multiplikation und Division; schriftliche Verfahren; Produkte und Quotienten
Einführung von Potenzen; Quadratzahlen
Verbindung der vier Grundrechenarten; Term; Rechengesetze, Rechenregeln, Regeln für vorteilhaftes Rechnen (Summanden und Faktoren vertauschen, Klammern setzen in Summen und Produkten, Punkt vor Strich, Rechnungen mit Klammern, Rechnungen mit Potenzen); Überschlagsrechnen
Terme beschreiben; aus Beschreibungen Terme ableiten
einfache Gleichungen und Ungleichungen durch Probieren lösen; grundlegende Mengenbegriffe
Sachaufgaben lösen

Größen; Maßzahl und Maßeinheit
Größen messen, verschiedene Messinstrumente kennen lernen
Maßstab
mit Größen rechnen (Komma nur als Trennzeichen zwischen Dezimalen und Vielfachen der Einheit);
Umwandlung in die kleinere bzw. größere Einheit; Größenangaben auch in gemischter Schreibweise und Kommaschreibweise (Umrechnung); Addition und Subtraktion (nicht in Kommaschreibweise)
Sachaufgaben lösen, einfache Dreisatzaufgaben

Strecke, Halbgerade, Gerade, Kreislinie, Punkt
Quadrat, Rechteck, Dreieck, Vieleck, Kreisfläche

[Konstruktionen]
Würfel, Quader, Prisma, Pyramide, Zylinder, Kegel, Kugel
Netze von Würfeln und Quadern
Länge einer Strecke; Umfang von Rechteck und Quadrat
symmetrische Figuren
senkrechte und parallele Geraden
Figuren im Gitternetz zeichnen

Vergleich von Flächen mit ungenormten und genormten Einheiten
Messen von Flächen; Umrechnen von Flächeneinheiten
Flächeninhalt von Rechteck und Quadrat
Oberfläche von Quader und Würfel
Sachaufgaben

Vergleich von Rauminhalten mit ungenormten und genormten Einheiten
Messen von Rauminhalten; Umrechnung von Raumeinheiten
Volumen von Würfel und Quader

Teiler und Teilermengen
Teilbarkeitsregeln
Primfaktorzerlegung; größter gemeinsamer Teiler (ggT), kleinstes gemeinsames Vielfaches (kgV) anhand einfacher Zahlenbeispiele

Erfassen, Darstellen und Auswerten von Daten; absolute Häufigkeit
Durchführung und Auswertung von ein- und zweistufigen Zufallsversuchen (Laplace-Experiment)
Anbahnen des Abzählens mit Hilfe von Baumdiagrammen

Quelle: http://www.isb.bayern.de
[Stand: 11/2012]

Hinweis: Die Lerninhalte sind ein Auszug aus dem Lehrplan für bayerische Schulen. In anderen deutschen Bundesländern existieren teilweise weitere Schularten. Diese sind z.B.: