Lineare Funktionen - Aufgaben/Übungen 1105

Vorschau auf das Übungsblatt

1. Aufgabe

Die Punkte A(-4|4, 5) und B(3|1) bestimmen die Gerade g₁.

a) Ermittle die Funktionsgleichung von g₁ rechnerisch.

b) Die Gerade g₁ schneidet die x-Achse im Punkt S. Ermittle rechnerisch die Koordinaten von S.

c) Die Gerade g₁ wird an der x-Achse gespiegelt. Es entsteht die Gerade g₂.

d) Zeichne die beiden Geraden in ein Koordinatensystem mit der Längeneinheit 1 cm.

e) Zeichne die Gerade g₃, die durch die Funktionsgleichung 4y - 8x = 8 bestimmt ist, in das Koordinatensystem.

f) Überprüfe rechnerisch, ob die Punkte P(-2, 5|- 2, 5) und Q(1, 5|5) auf g₃ liegen.

2. Aufgabe

Die Punkte P(6|3, 5) und Q(-2|1, 5) legen die Gerade g₁ fest.

a) Bestimme die Funktionsgleichung für g₁ rechnerisch und zeichne den Funktionsgraphen in ein Koordinatensystem mit der Längeneinheit 1 cm.

b) Eine zweite Gerade g₂ mit Steigung m = 1, 5 verläuft durch den Punkt R(0|- 3). Zeichne g₂ in das Koordinatensystem und bestimme ihre Funktionsgleichung.

c) Berechne die Koordinaten des Schnittpunktes S der beiden Geraden.

d) Berechne die fehlende Koordinate von Punkt A(-2|?), der auf g₁ liegt.

e) Berechne die fehlende Koordinate von Punkt B(?|4, 5), der auf g₂ liegt.

3. Aufgabe

Forme zunächst in die Normalform um, bestimme dann jeweils den Schnittpunkt rechnerisch.

a) g₁ :  2y - x = -4 und g₂ :  y = 4 + x

b) g₁ :   - 6x - 3 = -3y und g₂ :  3y - 1, 5x - 12 = 0

4. Aufgabe

Gegeben ist die Gerade g₁ :  y = 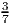x + 3.

a) Stelle die Funktionsgleichung für die Gerade g₂ auf, die parallel zu g₁ ist und durch den y-Achsenabschnitt -3 geht.

b) Stelle die Funktionsgleichung für die Gerade g₃ auf, die senkrecht zu g₁ ist und durch den Punkt S(0|3) geht.